|
|
Performance Visualization Tools : Programming on Multi-Core Processors |
|
Performance visualization tools such as Intel Thread Checker,
Intel Vtune Performance analyzer, Intel thread Debugger, Sun Studio, Etnus
totalview Debugger, Upshot, Jumpshot (Public domain) , and IBM Tools have been developed in
order to help the programmer to understand the behavior of a parallel (MPI/Pthreaded) program
and understand performance of application.
Example programs using different APIs. Compilation and execution
of Pthread programs, programs numerical and non-numerical computations
are discussed using
different thread APIs and understand Performance issues on mutli-core processors
|
Example 1.1
|
Write a Multi-threaded program to print Hello World . Analyze the
Performance using thread Visualization tool.
|
Example 1.2
|
Write a Multi-threaded (Pthreads) program to compute the value of PI pie function
f(x) = 4/(1+x2 ) between the limits 0 and 1 by Numerical Integration. Analyze
the Performance using thread Visualization tool.
|
Example 1.3
|
Write a Multi-threaded (OpenMP) program to compute the value of PI pie function
f(x) = 4/(1+x2 ) between the limits 0 and 1 by Numerical Integration.
Use OpenMP PARALLEL
directive. Analyze the Performance using thread
Visualization tool.
|
Example 1.4
|
Write a MPI program to compute the value of PI pie function
f(x) = 4/(1+x2 ) between the limits 0 and 1 by Numerical Integration.
you have to use MPI point-point communication library calls.
Analyze the Performance using MPI Visualization tool.
|
Example 1.5
|
Write a MPI-Pthreads program to calculate Infinity norm of a matrix using block striped
partitioning with row wise data distribution using p processe and t threads.
Analyze the Performance using thread Visualization tool.
|
Example 1.6
|
Write a MPI program to compute Matrix and Matrix Multiplication using block checkerboard
partitioning and MPI Cartesian topology. Analyze the Performance using MPI
Visualization tool. (Assignment)
|
(Source - References :
Books
Multi-threading
OpenMP -
[MCMPI-06],
[MCMPI-07], [MCMPI-09], [MCMPI-12], [MCMTh-15], [MCMTh-21], [MCBW-44],
[MCOMP-01],[MCOMP-02],[MCOMP-04], [MCOMP-12], [MCOMP-19],
[MCOMP-25])
|
|
Description of Muli-threaded (PThreads/OpenMP); MPI & MPI-Pthread
Programs |
Example 1.1:
|
Write an Multi-threaded program to print Hello World
and analyze the Performance using thread Visualization tool.
(Download source code :
tools-pthreads-hello-world.c)
|
- Objective
- Description
This is a very simple program to get the feel of threads and to get a view of how threads actually work. The implementation is as follows: The main thread creates two child threads. These threads print the words
Hello and World! individually. Though there is no actual parallelism involved, this is
just to demonstrate the working of threads. It is to be however noted that depending on the system load and
the implementation of Pthreads Standard, the message may not always be "Hello World!". It can be
"World! Hello"
depending on which thread is scheduled to execute first. This also demonstrates the use of "Pthread_join".
- Input
-
Output
|
| |
|
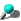Example 1.2:
|
Write an Multi-threaded program to compute the value of PI function by numerical integration of a
function f(x) = 4/(1+x2 ) between the limits 0 and 1.
(Download source code :
tools-pthread-num-int-pie.c)
|
- Objective
Write a Multi-threaded program to compute the value of PI function by numerical integration of a
function f(x) = 4/(1+x2 ) between the limits 0 and 1 using p processes and t threads
- Description
This program computes the value of PI over a given interval using Numerical integration.
All the threads determine the number of intervals to be calculated by it. The master thread assigns an
interval to each thread.
Threaded APIs provide support for implementing critical sections and atmoic operations using
mutex-locks (mutual exclusision locks).
Each thread calculates its part of the interval and finally adds it up to the result variable.
Mutex-Locks have two states : locked and unlocked. At any point of time, only one thread can
lock a mutex lock.
Each thread
locks a mutex before doing the same to guarantee the atomicity of the operation.
The Mutex-lock is an atomic operation generally associated with a piece of code that manipulates
shared data.To access the shared data, a thread must first try to acquire a mutex-lock. If the mutex-lock
is already locked, the process trying to acquire the lock is blocked.
- Input
Output
| |
|
- Objective
Write an OpenMP program to compute the value of PI by numerical
integration of a function f(x) = 4/(1+x*x ) between the limits 0
and 1 using OpenMP PARALLEL directive.
- Description
There are several approaches to parallelizing a serial program. One
approach is to partition the data among the threads.
That is we partition the interval of integration [0,1] among
the threads, and each thread estimates local integral over its own
subinterval. The local calculations produced by the
individual threads are combined to produce the final result.
To perform this integration numerically, divide the interval from
0 to 1 into n subintervals and add up the areas of the rectangles
as shown in the Figure 1 (n = 5). Large values of n
give more accurate approximations of PI value.
Fig. 1 : Numerical Integration of PI
function
In this program
OpenMP PARALLEL FOR directive, and CRITICAL section is
used. The CRITICAL directive specifies a region of program that
must be executed by only one thread at a time. If a thread is
currently executing inside a CRITICAL region and another
thread reaches that CRITICAL region and attempts to execute
it, it will block until the first thread exits that CRITICAL
region.
- Input
- Output
|
| |
|
Example 1.4:
|
Write a MPI program to compute the value of PI function by numerical integration of a
function f(x) = 4/(1+x2 ) between the limits 0 and 1 using MPI point-to-point
communication library calls. Analyze the
Performance using MPI Visualization tool.
(Download source code :
tools-numint-pie-pt-to-pt.c)
|
- Objective
Write a MPI program to compute the value of pie function by numerical integration of a
function
f(x) = 4/(1+x2) between the limits 0 and 1 using MPI point-to-point
communication library calls.
- Description
In this example, partition the interval of
integration [0,1] among the processes is done, and each process estimates local integral over
its own subinterval. The local calculations produced by the individual
processes are combined to produce the final result. Each process sends its integral to process 0,
which adds them and prints the result.
To perform this integration numerically, divide the interval from 0 to 1 into n
subintervals and add up the areas of the rectangles as shown in the Figure 2 (n
= 5). Large values of n give more accurate approximations of pi
. Use MPI point-to-point communication library calls.
Figure 2 Numerical integration of pie function
We assume that n is total number of subintervals, p is the number
of processes and p < n. One simple way to distribute the total
number of subintervals to each process is to divide n by p. There
are two kinds of mappings that balance the load. One is a block mapping,
partitions the array elements into blocks of consecutive entries and assigns
the block to the processes. The other mapping is a cyclic mapping. It
assigns the first element to the first process, the second element to the
second, and so on. If n > p, we get back to the first process,
and repeat the assignment process for remaining elements. This process is
repeated until all the elements are assigned. We have used a cyclic mapping
for partition of interval [0,1] onto p processes.
- Input
Process with rank0 reads the input parameter n, the number of intervals on
command line.
- Output
|
| |
|
Example 1.5:
|
Write an MPI-Pthreads program to calculate Infinity norm of a matrix using block striped
partitioning with row wise data distribution. Analyze the
Performance using thread Visualization tool.
(Download source code :
tools-mpi-pthreads-infinity-norm.c )
|
- Objective
Write an MPI-Pthreads program to calculate Infinity norm of a matrix using block striped
partitioning with row wise data distribution using p processe and t threads
- Description
Infinity Norm of a Matrix: The Row-Wise infinity norm of a matrix is defined to be the maximum of sums of
absolute values of elements in a row, over all rows.
After the initial validity checks, each process reads the input matrix and determines the number of rows
to be operated by it. Using its rank, each process determines the specific rows to be operated by it.
After the distribution of rows, the main thread on each process creates the child threads as the number of rows
it is to operate. Each thread operates on the specified row and calculates the sum of the absolute values of the elements
and updates a common variable. After all the threads on a process complete their share of work,
the common variable holds the maximum value of the rows assigned to it. Finally, the Root process
determines the infinity norm using a Collective MPI call, MPI_Reduce and prints the value.
- Input
- Output
|
| |
|
Example 1.6: |
Write a MPI program to compute the matrix into matrix multiplication using Checker-Board
Partitoning of input Matrices.Analyze the
Performance using thread Visualization tool.
|
- Objective
Write an MPI-Pthreads program to compute the Matrix into Matrix multiplication using Checker-Board
Partitoning of input Matrices. using p processe and t threads
- Description
In checkerboard partitioning, the matrix is divided into smaller square or rectangular blocks
(submatrices) that are distributed among processes. A checkerboard partitioning splits both the rows and the
columns of the matrix, so no process is assigned any complete row or column.
Like striping partitioning, checkerboard partitioning can be block or cyclic.
- Input
The input file holding the two square matrices (Number of Rows, Columns of the matrix)
- Output
|
| |
|
|
| |
|
