|
Programming on Multi-Core Processors Using OpenMP APIs |
|
The OpenMP API is used for writing portable multi-threaded applications written in Fortran, C and C++ languages.
The OpenMP programming model plays a key role by providing an easy method for threading applications without burdening
the programmer with the complications of creating, synchronizing load balancing, and destroying threads.
The OpenMP model provides a platform independent set of compiler pragmas, directives, function calls, and environment
variables that explicitly instruct the compiler how and where to use the parallelism in the application.
Example programs using
compiler pragmas, directives, function calls, and environment variables, Compilation and execution
of OpenMP programs, programs numerical and non-numerical computations
are discussed.
|
Example 2.1
|
Write a OpenMP program to Compute the value of pie value by Numerical Integration
using OpenMP PARALLEL directive.
|
Example 2.2
|
Compute the value of PI function by Numerical Integration using OpenMP REDUCTION clause.
|
Example 2.3
|
Write a OpenMP program to transpose of a matrix using OpenMP PARALLEL DO directive.
|
Example 2.4
|
Write a OpenMP program to Matrix vector multiplication using OpenMP PARALLEL directive.
|
Example 2.5
|
Write a OpenMP program to Matrix matrix multiplication using OpenMP PARALLEL FOR directive.
|
Example 2.6
|
Write a OpenMP program for Matrix - Matrix Multiplication using OpenMP one PARALLEL for directive and Private Clause
|
Example 2.7
|
OpenMP program : Matrix Matrix multiplication based on nested loop
using OpenMP PARALLEL section, SHARED, PRIVATE clauses.
|
Example 2.8
|
OpenMP program :Matrix - Matrix Multiplication using OpenMP PARALLEL for directive and Private and Schedule Clause
|
(Source - References :
Books
Multi-threading
OpenMP
-[MCMTh-01], [MCMTh-02], [MCMTh-I03], [MCMTh-05], [MCMTh-09], [MCMTh-11],
[MCMTh-15], [MCMTh-21], [MCBW-44], [MCOMP-01], [MCOMP-02],
[MCOMP-04], [MCOMP-12], [MCOMP-19], [MCOMP-25])
|
|
Description of OpenMP Programs |
|
Example 2.1 :
Compute the value of PI
function by Numerical Integration using OpenMP PARALLEL
directive.
(Download source code :
omp-pi-calculation.c
/
omp-pi-calculation.f
)
|
- Objective
Write an OpenMP program to compute the value of PI by numerical
integration of a function f(x) = 4/(1+x*x ) between the limits 0
and 1 using OpenMP PARALLEL directive.
- Description
There are several approaches to parallelizing a serial program. One
approach is to partition the data among the threads.
That is we partition the interval of integration [0,1] among
the threads, and each thread estimates local integral over its own
subinterval. The local calculations produced by the
individual threads are combined to produce the final result.
To perform this integration numerically, divide the interval from
0 to 1 into n subintervals and add up the areas of the rectangles
as shown in the Figure 1 (n = 5). Large values of n
give more accurate approximations of PI value.
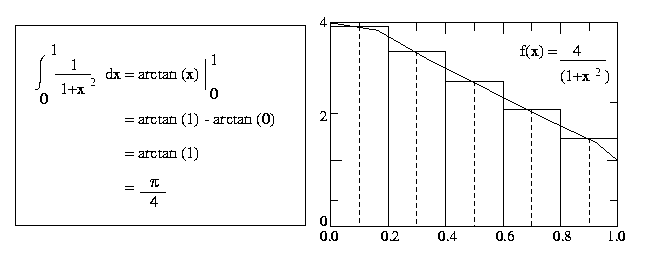
Fig. 1 : Numerical Integration of PI
function
In this program
OpenMP PARALLEL FOR directive, and CRITICAL section is
used. The CRITICAL directive specifies a region of program that
must be executed by only one thread at a time. If a thread is
currently executing inside a CRITICAL region and another
thread reaches that CRITICAL region and attempts to execute
it, it will block until the first thread exits that CRITICAL
region.
- Input
Number of threads and Number of intervals.
- Output
Computed value of pie and time taken for the computation.

|
|
Example 2.2 :
Compute the value of pie
function by Numerical Integration using OpenMP REDUCTION clause
(Download source code :
omp-pi-calculation-reduction.c
/
omp-pi-calculation-reduction.f
)
|
- Objective
Write an OpenMP program to compute the value of PI by
numerical integration of a function f(x) = 4/(1+x*x ) between
the limits 0 and 1 using OpenMP REDUCTION Operation.
- Description
PI value is computed using OpenMP PARALLEL
FOR directive and REDUCTION clause. Reductions are a
common type of operation. OpenMP includes a reduction data
scope clause just to handle the variable. In reduction, we repeatedly
apply a binary operator to a variable, and
store the result back in the variable. When a program performs a
reduction using a commutative-associative operator, reduction can
be easily parallelized by adding a REDUCTION clause to the PARALLEL
FOR directive. In REDUCTION a private copy for each list
variable is created for each thread. At the end of the reduction,
the reduction operator is applied to all private copies of the
shared variable, and the final result is written to the global
shared variable. In this example we have
added the clause REDUCTION ( + : Local Sum), which tells the compiler
that LocalSum is the target of a sum reduction operation.
- Input
Number of threads and Number of intervals
- Output
Computed value of pie and time taken for the computation.

|
|
Example 2.3 :
Transpose of a matrix using OpenMP PARALLEL
DO directive
(Download source code :
omp-matrix-transpose.c
/
omp-matrix-transpose.f
)
|
-
Objective
Write a OpenMP program for transpose of a matrix
using OpenMP PARALLEL DO directive and measure the performance
-
Description
In this example we have shown how to parallelize
the nested loop. Loop nest can contain more than one loop, and arrays
can have more than one dimension. The two-deep loop nest in Transpose
of a matrix , changes the corresponding rows and columns of the
input matrix to columns and rows of the output matrix i.e. Trans
[j][i] = Mat[i][j]. Usually we want to parallelize the outermost
loop in such nest. For correctness, there must not be a dependence
between any two statements executed in different iterations of parallelized
loop. In this example, we can safely parallelize the i loop because
each iteration of the loop changes row of input matrix to
corresponding column of the output matrix. In this example PARALLEL directive,
PRIVATE clauses and FOR directive are used.
-
Input
Number of threads and Size of matrix
-
Output
Time taken for the matrix computations.
|
|
Example 2.4 :
Matrix vector multiplication using OpenMP PARALLEL
directive.
(Download source code :
omp-matvect-mult.c
/
omp-matvect-mult.f
)
|
- Objective
Write an OpenMP program for computing matrix vector multiplication
using OpenMP PARALLEL directive.
- Description
Each row of matrix A is multiplied with elements of vector B(i) and
the resultant vector is stored in vector C(i). It is assumed
that number of columns of the matrix A and size of the vector
are same. This example demonstrates the use of OpenMP
loop of work-sharing construct i.e. distribution of columns of Matrix
A. The ORDERED section directive is used to improve an order across
the elements of C(i). Matrix A and vector B are generated
automatically.
- Input
Number of threads , Size of Matrix and Size of the Vector.
- Output
Each thread computes the multiplication and prints the time taken for the computation.C(i)
|
|
Example 2.5 :
Matrix - Matrix multiplication using OpenMP PARALLEL FOR directive.
(Download source code :
omp-matmat-mult.c
/
omp-matmat-mult.f
)
|
-
Objective
Write a OpenMP program for matrix-matrix multiplication
using OpenMP PARALLEL
FOR directive and measure the performance.
-
Description
In this example we have shown how to parallelize
the nested loop. Loop nest can contain more than one loop, and arrays
can have more than one dimension. The three-deep loop nest in Matrix-matrix
multiplication, computes the product of two matrices C =
A * B. Usually we want to parallelize the outermost
loop in such nest. For correctness, there must not be a dependence
between any two statements executed in different iterations of parallelized
loop. However, there may be dependences between statements executed
with in a single iteration of the parallel loop, including dependences
between different iterations of an inner, serial loop. In this,
example, we can safely parallelize the j loop because each iteration
of the loop computes one column FinalMatrix(1:MatrixSize,j) of the
product and does not access elements of FinalMatrix that are outside
that column. The dependence on FinalMatrix(i,j) in the serial
k
loop does not inhibit parallelization. In this example PARALLEL
FOR directive, SHARED and PRIVATE clause are used.
-
Input
Number of threads , Size of matrix.
-
Output
Time taken
for Matrix-Matrix computations.

|
|
Example 2.6 :
Matrix Matrix multiplication using OpenMP one PARALLEL for
directive and Private Clause. <
(Download source code :
omp-matmat-one-parallel.c
)
|
-
Objective
Write a OpenMP program for matrix-matrix multiplication using OpenMP PARALLEL
For directive and a PRIVATE clause.
-
Description
In this example we have shown how to parallelize the nested loop.
Loop nest can contain more than one loop, and arrays can have more than one dimension.
The three-deep loop nest in Matrix-matrix multiplication, computes the product of
two matrices C = A * B . Usually we want to parallelize the outermost loop in such nest.
For correctness, there must not be a dependence between any two statements executed in different iterations
of parallelized loop. However, there may be dependences between statements executed with in a single
iteration of the parallel loop, including dependences between different iterations of an inner, serial
loop. In this, example, we can safely parallelize the j loop because each iteration of the loop computes
one column FinalMatrix(1:MatrixSize,j) of the product and does not access elements of FinalMatrix that
are outside that column. The dependence on FinalMatrix(i,j) in the serial k loop does not
inhibit parallelization. In this example PARALLEL section and PRIVATE clause are used..
-
Input
Number of threads.
Size of matrix in terms of Class where
Class A : 1024
Class B : 2048
Class C : 4096
-
Output
Time taken for Matrix matrix computations and total memory utilized.

|
|
Example 2.7 :
Matrix Matrix multiplication based on nested loop
using OpenMP PARALLEL section, SHARED, PRIVATE clauses
(Download source code :
omp-matmat-three-parallel.c
)
|
-
Objective
Write a OpenMP program for matrix-matrix multiplication
using OpenMP three PARALLEL
for directive and a PRIVATE clause.
-
Description
In this example we have shown how to parallelize the nested loop. Loop nest
can contain more than one loop, and arrays can have more than one dimension.
The three-deep loop nest in Matrix-matrix multiplication, computes the product of
two matrices C = A * B. Usually we want to parallelize all the three loops in such nest.
For correctness, there must not be a dependence between any two statements executed in different
iterations of parallelized loop. However, there may be dependences between statements executed with
in a single iteration of the parallel loop, including dependences between different iterations of an inner,
serial loop. In this example PARALLEL section, SHARED, PRIVATE clause are used.
-
Input
Number of threads .
Size of matrix in terms of Class where
Class A : 1024
Class B : 2048
Class C : 4096
-
Output
Time taken for Matrix Matrix computations and the total memory utilized.

|
|
Example 2.8 :
Matrix Matrix multiplication
using OpenMP parallel or directive Private and Schedule
Clauses
(Download source code :
omp-matmat-static-parallel.c
)
|
-
Objective
Write a OpenMP program for matrix-matrix multiplication using OpenMP three PARALLEL
For directive and PRIVATE and SCHEDULE clause. .
-
Description
In this example we have shown how to parallelize the nested loop. Loop nest can contain more than one loop, and arrays can have more than one dimension. The three-deep loop nest in Matrix-matrix multiplication, computes the product of two matrices C = A * B. Iterations of the parallel loop will be distributed in equal sized blocks to each thread in the team (SCHEDULE STATIC).In this example PARALLEL FOR directive, PRIVATE ,SCHEDULE clause are used
-
Input
Number of threads .
Size of matrix in terms of Class where
Class A : 1024
Class B : 2048
Class C : 4096
-
Output
Time taken for Matrix matrix Computations and total memory utilized.
|
|
| |
|
