hyPACK-2013 Mode 1 : Parallel Programming Using MPI C++ Library Calls

Write MPI C++ Program (SPMD) to get started

Write MPI C++ program (MPMD) to get started.

Write MPI C++ program to find sum of n integers on Parallel Processing Platform. You have to use MPI point-to-point blocking communication library calls

Write MPI C++ program to find sum of n integers on a Parallel Computing System in which procesors are connected with linear array topology and use MPI point-to-point blocking communication library calls (Assignment Question)

Write MPI C++ program to find sum of n integers on a Parallel Computing System in which procesors are connected with ring topology and use MPI point-to-point blocking communication library calls

Write MPI C++ program to find sum of n integers on a Parallel Computing System in which procesors are connected with tree topology (Associative-fan-in rule for tree can be assumed) and use MPI point-to-point blocking communication library callson library calls.

Write MPI C++ program to compute the value of PI by numerical integration using MPI point-to-point blocking communication library calls.

Write MPI C++ program for prefix sum (scan operation) calculation using MPI point-to-point blocking communication library calls. ( Assignment Question )

Write MPI C++ program to find sum of n integers on a Parallel Computing System in which procesors are connected with tree topology (Associative-fan-in rule for tree can be assumed) and use MPI point-to-point non-blocking communication library calls. (Assignment Question)

• Objective

Write a MPI C++ program to print "Hello World"


• Description

Process with rank k ( k = 1, 2, ....., p-1) will send"Hello World" message to process with rank0. Process with rank0receives the message and prints it. You have to use MPI point-to-point blocking communication library calls (MPI::COMM_WORLD.Send and MPI::COMM_WORLD.Recv) to write this program.

• Input  

None

• Output  

Process with rank 0 prints the following message with each of the other process's Rank Numbers (i.e. rank = 1,2, ..., p-1). Hello World from Process's rank where rank = 1,2, ..., p-1

• Objective

Write a MPI C++ program to print "Hello World"

• Description

Process with rank k ( k = 1, 2, ....., p-1) will send " Hello World" message to process with rank 0.Process with rank 0 receives the message and prints it. MPI point-to-point communication library calls (MPI::COMM_WORLD.Send and MPI::COMM_WORLD.Recv) have been used in this program. The master process is responsible for receiving the "hello message" from all participating processes (i.e slaves). On the other hand, the slave program is responsible for sending "Hello Message" to the master process. All slaves perform identical tasks. In ohterwords, the slave program send the result back to the master process.

• Input  

None

• Output  

Process with rank 0 prints the following message with each of the other process's Rank Numbers (i.e. rank = 1,2, ..., p-1). Hello World From process rank where rank = 1,2, .....p-1

• Objective

Write a MPI program to find sum of n integers on p processors of Message Passing cluster

• Description

Each process with rank greater than 0 sends the value of its rank to the process with rank 0. Process with rank 0 receives the values from each process and calculate the sum. Finally, process with rank 0 prints the sum.

• Input  

For input data, let each process uses its identifying number, i.e. the value of its rank. For example, process with rank 0 uses the number 0, process with rank 1 uses the number 1, etc.

• Output  

Process with rank 0 prints the final sum.

• Objective

MPI program to find sum of n integers on a Parallel Processing platform in which processors are connected by linear array topology.

• Description

In linear array interconnection network, each processor ( except the processor at the end ) has a direct communication link to the immediate next processor. A simple way of communicating a message between processors is, by repeatedly passing message to the processor immediately to either right or left , until it reaches its destination, i.e. last processor in the linear array. A simple way to connect processors is illustrated in Figure 1.



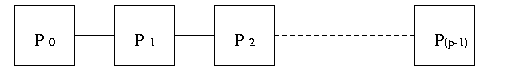Figure 1 Parallel Computing system - Processors are connected by Linear Array topology



All the processes are involved in communication. The processes with rank k (k is greater than 0) receives the accumulated or partial sum from the previous process with rank k-1. Finally, process with rank p-1 prints the final sum.

• Input  

For input data,let each process use its identifying number, i.e. the value of its rank. For example, process with rank 0 uses the number 0, process with rank 1 uses the number 1, etc.

• Output  

Process with rank p-1 prints the final sum.

• Objective

Write a MPI program to find sum of n values using p processors of cluster. Assume that p processors are arranged in ring topology.

• Description

In linear array interconnection network ( Refer Example 1.4 for more details on linear array topology ) with a wraparound connection is called as a ring. A wraparound connection is often provided between the processors at the end.A simple way of communicating a message between processors is, by repeatedly passing message to the processor immediately to either right or left; depending on which direction yield a shorter path, until it reaches its destination, i.e., first processor in the ring.

All the processes are involved in communication. The process with rank k (k is greater than 0) receives the accumulated or partial sum from the previous process with rank k-1. Process with rank p-1 sends the final sum to process with rank 0. Finally, process with rank 0 prints the final sum.

• Input  

For input data, let each process use its identifying number, i.e. the value of its rank. For example, process with rank 0 uses the number 0, process with rank 1 uses the number 1, etc.

• Output  

Process with rank 0 prints the final sum.

• Objective

Write a MPI program to find sum of n ( n = 2 ⁱ ; i = 3) integers on p (p=n) processors of cluster using associative fan-in rule.

• Description

The first step is to group the total number of processors in ordered pairs such as (P₀, P₁), (P₂, p₃), (P₄, P₅), (P₆, p₇), .................., (P_p-2, P_p-1). Then compute the partial sums in all pairs of processors using MPI point-to-point blocking communication and accumulate the partial sum on the processors P₀, P₂, ....,P_p-2. For example, the processor P_i (i is even) computes the partial sum for the pair (P_i, P_i+1) by performing MPI point-to-point blocking communication library calls.


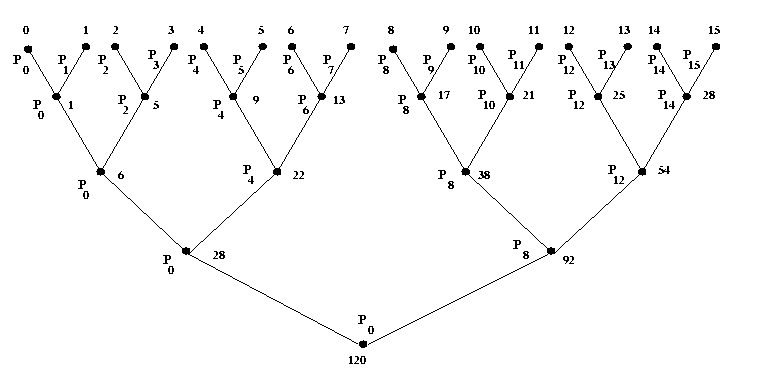Figure 2. Tree Structure for sum of n integers by Associativ fan-in rule

In the second step, consider the pair of processors (P₀, P₂), (P₄, P₆), ................., (P_p-4, P_p-2) obtain the new partial sum by considering the existing accumulated partial sums on the processors P₀, P₂, P₄, ..., P₈as explained in the previous step. This procedure is repeated till two processors are left out and finally accumulate the global sum on the processor P₀.In this example, MPI point-to-point blocking communication library calls such as,MPI::COMM_WORLD.Send and MPI::COMM_WORLD.Recv, are used. An example of associative fan-in rule is described as a tree structure in the Figure 2 for n= 16

• Input

For input data, let each process use its identifying number, i.e. the value of its rank. For example, process with rank 0 uses the number 0, process with rank 1 uses the number 1, etc.

• Input  

For input data, let each process use its identifying number, i.e. the value of its rank. For example, process with rank 0 uses the number 0, process with rank 1 uses the number 1, etc.

• Output  

process with rank 0 prints the final sum.

• Objective

Write a MPI program to compute the value of pie function by numerical integration of a function f(x) = 4/(1+x ² ) between the limits 0 and 1.

• Description

There are several approaches to parallelizing a serial program. One approach is to partition the data among the processes. That is we partition the interval of integration [0,1] among the processes, and each process estimates local integral over its own subinterval. The local calculations produced by the individual processes are combined to produce the final result. Each process sends its integral to process 0, which adds them and prints the result.

To perform this integration numerically, divide the interval from 0 to 1 into n subintervals and add up the areas of the rectangles as shown in the Figure 3 (n = 5). Large values of n give more accurate approximations of pi . Use MPI point-to-point communication library calls.



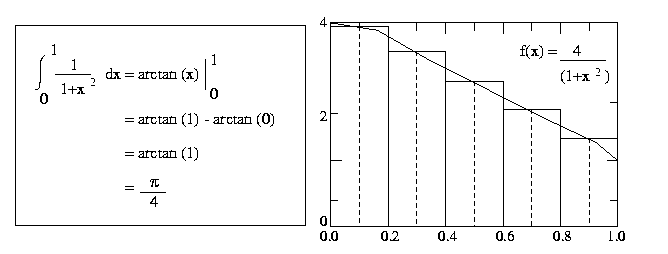
Figure 3 Numerical integration of pie function

We assume that n is total number of subintervals, p is the number of processes and p < n. One simple way to distribute the total number of subintervals to each process is to dividen by p. There are two kinds of mappings that balance the load. One is a block mapping, partitions the array elements into blocks of consecutive entries and assigns the block to the processes. The other mapping is a cyclic mapping. It assigns the first element to the first process, the second element to the second, and so on. If n > p, we get back to the first process, and repeat the assignment process for remaining elements. This process is repeated until all the elements are assigned. We have used a cyclic mapping for partition of interval [0,1] ontop processes.

• Input

For input data, let each process use its identifying number, i.e. the value of its rank. For example, process with rank 0 uses the number 0, process with rank 1 uses the number 1, etc.

• Input  

Process with rank0 reads the input parameter n, the number of intervals on command line.


• Output  

Process with rank 0 prints the computed value of pi function.

• Objective

Write a MPI program to find sum of n ( n = 2 ⁱ ; i = 3) integers on p (p=n) processors of cluster using associative fan-in rule.

• Description

The first step is to group the total number of processors in ordered pairs such as (P₀, P₁), (P₂, p₃), (P₄, P₅), (P₆, p₇), .................., (P_p-2, P_p-1). Then compute the partial sums in all pairs of processors using MPI point-to-point blocking communication and accumulate the partial sum on the processors P₀, P₂, ....,P_p-2. For example, the processor P_i (i is even) computes the partial sum for the pair (P_i, P_i+1) by performing MPI point-to-point blocking communication library calls.


Figure 2. Tree Structure for sum of n integers by Associativ fan-in rule

In the second step, consider the pair of processors (P₀, P₂), (P₄, P₆), ................., (P_p-4, P_p-2) obtain the new partial sum by considering the existing accumulated partial sums on the processors P₀, P₂, P₄, ..., P₈as explained in the previous step. This procedure is repeated till two processors are left out and finally accumulate the global sum on the processor P₀.In this example, MPI point-to-point non-blocking communication library calls such as,MPI::COMM_WORLD.ISend and MPI::COMM_WORLD.IRecv, can be used. An example of associative fan-in rule is described as a tree structure in the Figure 2 for n= 16

• Input

For input data, let each process use its identifying number, i.e. the value of its rank. For example, process with rank 0 uses the number 0, process with rank 1 uses the number 1, etc.

Process with rank0 reads the input parameter n, the number of intervals on command line.


• Output  

process with rank 0 prints the final sum.