NVIDIA\92s Compute Unified Device Architecture (CUDA) is a soft- ware platform for massively parallel high-performance computing on the company's powerful GPUs. NVIDIA\92s software CUDA programming model effectively use GPUs which could be harnessed for tasks other than graphics, achieving teraflops of computing power. CUDA Programming model automatically manages the threads and it is significantly differs from single threaded CPU code and to some extent even the parallel code. Efficient CUDA programs exploit both thread parallelism within a thread block and coarser block parallelism across thread blocks. Because only threads within the same block can cooperate via shared memory and thread synchronization, programmers must partition computation into multiple blocks.

• Objective

  Write test programs using CUBLAS1, CUBLAS2, CUBLAS3 library function calls (CudaBlas Library \96 wrapper functions for efficient and simple usage of CUBLAS
  

• Objective

  Write a program to perform vector vector multiplication using CUBLAS1 library function call.
  

• Description

  The input vectors are generated on Host-CPU and transfer the vectors to Device-GPU for vector multiplication using CUBALS1 library call. The final output value is transferred back to Host-CPU.

• Input

length of input vectors & generation of elements

• Output

Scalar value

• Objective

  Write a Program for multiplication of a scalar with a vector and add the resultant vector to a vector using CUBLAS1 library function calls
  

• Description

  Two input vectors ( first, second ) and a scalar value is generated on Host-CPU and multiplication of scalar value with vector is done on Device-GPU. Addition of resultant vector and second vector is computed on Device-GPU to obtain the solution vector, which is transferred back to Host-CPU.

• Input

length of input vectors and elements of the vector.

• Output

Solution Vector

• Objective

  Write a program to perform matrix vector multiplication using CUBLAS2 library function call.
  

• Description

  The input matrix and input vector is generated on the Host-CPU. In simple algorithm, the input matrix is partitoned as per Grid of thread blocks. Each thread reads one row of the matrix and performs computation with column of the vector to obtain resultant vector on Device-GPU. The resultant solution vector is transferred back to Host-CPU. The CUBLAS2 library call performs comptuation on the Device-GPU.

• Input

Matrix Size

• Output

execution time in seconds,Gflops achieved

• Objective

  Write a Program to perform matrix matrix multiplication using CUBLAS3 library function calls.
  

• Description

  Two input matrices are generated on the Host-CPU. In simple algorithm, the input matrix is partitoned as per Grid of thread blocks. Each thread reads one row of the matrix and performs computation with one column of the another matrix and compute the correspodning elements of resultant marix on Device-GPU. The resultant matrix is transferred back to Host-CPU. The CUBLAS3 library call performs computation on the Device-GPU.

• Input

Matrix Size

• Output

execution time in seconds,Gflops achieved

• Objective

  Write a CUBLAS CUDA program, for solving system of linear equations [A]{x} = {b} on CUDA enabled NVIDIA programming environment using Jacobi method
  

• Description

  The Jacobi iterative method is one of the simplest iterative techniques to solve system of linear equations. The i^th equation of a system of linear equations [A]{x}={b} is
  

  

  
  

  If all the diagonal elements of A are nonzero (or are made nonzero by permuting the rows and columns of A), we can rewrite equation (1)

  
  

  

  
  

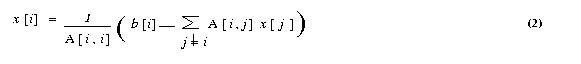
  The Jacobi method starts with an initial guess x₀ for the solution vector x. This initial vector x₀ is used in the right-hand side of equation (2) to arrive at the next approximation x₁ to the solution vector. The vector x₁ is then used in the right hand side of equation (2), and the process continues until a close enough approximation to the actual solution is found. A typical iteration step in the Jacobi method is

  

  
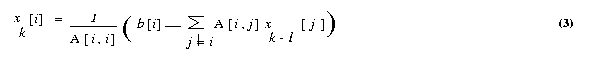
  We now express the iteration step of equation 3 in terms of residual r_k. Equation (3) can be rewritten as
  

  

  
  

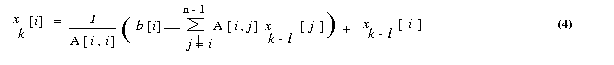
• Implementation The input matrix and the right hand-side vector, intial soultion vector is generated on Host-CPU and transferred to Device-GPU. In simple algorithm, the input matrix is partitoned as per Grid of thread blocks. Each thread reads one row of the matrix A and performs computation with vector and update the solution vector. Convergence of the solution is checked and the solution vector is transferred back to Host-CPU.
  
  
• Input

Size of Input Matrix and the Vector

• Output

The solution of matrix system of linear equations Ax = b

• Objective

  CUDA implementaiton for Conjugate Gradient Method to solve the system of linear equations [A]{x}={b}. Assume that A is symmetric positive definite matrix.

• Description

  Description of conjugate gradient method :
  
  The conjugate gradient (CG) method is an example of minimizing method. A real n x n matrix A is positive definite if x^T A x > {0} for any n x 1 real, nonzero vector x. For a symmetric positive definite matrix A, the unique vector x that minimizes the quadratic functional
  
  f(x) = (1/2)x^TAx-x^Tb 
  
  is the solution to the system Ax = b, here x and b are n x 1 vectors. It is not particularly relevant when n is very large, since the conjugating time for that number of iterations is usually prohibitive and the property does not hold in presence of rounding errors. The reason is that the gradient of functional f (x) is Ax - b, which is zero when f (x) is minimum. The gradient of a function is a n x 1 vector. We explain some important steps in the algorithm. An iteration of a minimization method is of the form
  
  

  x_k+1 = x_k  + tau_kd_k     (1) 
   
  where tau_k is a scalar step size and d_kis the direction vector, d_k is a descent direction for f at x.  We now consider the problem of determining tau_k, given x_k and d_k, so that f(x) is minimized on the line x = x_k + tau_k d_k, for tau_k. The function f(x_k+ tau d_k) is quadratic in tau, and its minimization leads to the condition
  
  tau _k =  g_k^Tg_k / d_k^TAd_k ,    (2) 
  where g_k=Ax_k - b is the gradient (residue)  vector after k iterations. The residual need not be computed explicitly in each iteration because it can be computed incrementally by using its value from the previous iteration. In the (k+1)^th iteration, the residual g_k+1 can be expressed as follows: 
  
       g_k+1  = Ax_k+1 - b        = A(x_k+ tau_k d_k) - b 
       = Ax_k- b + tau_k Ad_k  
  
       = g_k + tau_k Ad_k     (3)
  
  

  Thus, the only matrix-vector product computed in each iteration is Ad_k, which is already required to compute tau_k  in the equation (2). If A is a symmetric positive definite matrix and d₁, d_2,..., d_n are direction vectors that are conjugate with respect to A (that is, d_i^T Ad_j=0 for all 0<n, j<=n, i!=j), then x_k+1 in the Equation (1) converges to the solution of Ax = bin at most n iterations, assuming no rounding errors.
  
  In practice, however, the number of iterations that yields an acceptable approximation to the solution is much smaller than n.  It  also  makes the gradient at x_k+1 orthogonal to search direction, i.e  d_k^T g_k+1  = 0.  Now we suppose that the search directions are determined by an iteration of the form 
  
  

  d_k+1 = -g_k+1+ beta_k d_k      (4)
  
  

  where d₀ = -g₀  and beta₀, beta₁ , ...... remain to be determined. We find the new search direction in the  plane spanned by the gradient at the most recent point and previous search direction. The parameter beta_k+1is determined by following equation
  
  

  Beta_k+1 = g^T_k+1Ad_k/ d^T_kAd_k     (5)
  And, one can derive orthogonality relations
    g^T_kg _l= 0 (l != k);                 d^T_kAd_l = 0 (l !=k)
  
  The derivation of the above equation (5)  and orthogonality relations is beyond the scope of this document. For details please refer [ ]. Using equation (3) and orthogonality relations, the equation (5)  can be further reduced to
  
  Beta_k+1 = g^T_k+1g_k+1/ g^T_kg_k<     (6)
  
  

  The above equations (1) to (6) lead to CG algorithm. The algorithm terminates when the square of the Euclidean vector norm of gradient (residual) falls below a predetermined tolerance value.  Although all of the versions of the conjugate gradient method obtained by combining the formulas for g_k, Beta_k, and tau_k in various ways are mathematically equivalent, their computer implementation is not. The following version is compared with respect to computational labor, storage requirements, and accuracy. The following sequence of steps are widely accepted.
  

  1. tau _k         =  g_k^Tg_k / d_k^TAd_k 
  2. x_k+1        = x_k  + tau_k d_k 
  3. g_k+1        =  g_k + tau_k Ad_k  
  4. Beta_k+1 = g^T_k+1g_k+1/ g^T_kg_k 
  5. d_k+1        = -g_k+1 + Beta_k d_k 
  
  where k = 0, 1, 2, .......... Initially we choose x₀, calculate g₀ = Ax₀ - b , and put d₀= -g₀ 
  
  The computer implementation of this algorithm is explained as follows :
  
  void CongugateGradient(float x₀ [ ], float b [ ], float d) 
      { 
         float    g, Delta0, Delta1, beta; 
         float    temp, tau; 
         int        iteration;
         iteration = 0;
         x   = x_0;          g = b; 
         g = A x - g; 
         Delta0 = g^T * g;   
         if ( Delta0 <= EPSILON) 
             return;  
         d = -g; 
         do { 
            iteration = iteration + 1; 
            temp = A * d;  
            tau = Delta0 / d^T  * temp;  
            x = x + tau * d;  
            g = g + tau * temp;  
            Delta1 = g^T  * g;
            if ( Delta1 <= EPSILON )  
                   break; 
            beta = Delta1 / Delta0;  
            Delta0 = Delta1;  
            d = -g + beta * d;  
        } while(Delta0 > EPSILON && Iteration < MAX_ITERATIONS);
         return;
   

  Regarding one-dimensional arrays of size n x 1 are required for temp, g, x, d. The storage requirement for matrix. A is depends upon the structure ( dense, band, sparse ) of the matrix.The two dimensional n x n array is the simplest structure to store matrix A. For large sparse matrix A this structure wastes a large amount of storage space, for such matrix A suitable storage scheme should be used.
  
  

• The preconditioned conjugate gradient algorithm  




Let C be a positive definite matrix factored in the form C = E E^T, and let the quadratic functional 


f(x) = (1/2)x^TAx - x^Tb + C , 
We define second quadratic functional g(y) by the transformation y = E^Tx,

g(x) = g(E^-Ty) = (1/2)y^TA^*y - y^Tb ^* + C^*         where A ^* = E^-1AE^-T, b^* = E^-1b, C^* = C. 
Here, A^* is symmetric and positive definite. The similarity transformation

E^-TA^*E^T = E^-TE^-1A = C^-1A 

reveals that A^* and A have same eigen values. If C can be found such that the condition number of the matrix A^* is less than the condition number of the matrix A, then the rate of convergence of the preconditioned method is better than that of conjugate gradient method. We call C the preconditioning matrix, A^* the preconditioned matrix, We assume that the matrix C = EE^T is positive definite, since E is nonsingular by assumption. If the coefficient matrix A has l distinct eigen values, the CG algorithm converges to the solution of the system Ax = b in at most l iterations (assuming no rounding errors). Therefore, if A has many distinct eigen values that vary widely in magnitude, the CG algorithm may require a large number of iterations to converge to an acceptable approximation to the solution.

The speed of convergence of the CG algorithm can be increased by preconditioning A with the congruence transformation A* = E^-1AE^-T where E is a nonsingular matrix. E is chosen such that A* has fewer distinct eigen values than A. The CG algorithm is then used to solve A* y =b*, where x =(E^T)^-1y . The resulting algorithm is called the preconditioned conjugate gradient (PCG) algorithm. The step performed in each iteration of the preconditioned conjugate gradient algorithm are as follows



1.   tau _k         =  g_k^Th_k / d_k^TAd_k 
2.   x_k+1       = x_k + tau_k d_k 
3.  g_k+1       =  g_k + tau_k Ad_k  
4.   h_k+1       =  C^-1g_k+1 
5. &nsbp; beta_k+1 = g^T_k+1h_k+1/ g^T_kh_k 
6.   d_k+1       = -h_k+1 + beta_k+1d_k

where k = 0, 1, 2, .......... Initially we choose x₀, calculate g₀ = Ax₀ - b, h₀= C^-1g₀ and d₀ = -h₀. The multiplication by C^-1 in step (4) is to be interpreted as solving a system of equations with coefficient matrix C. A source of preconditioning matrices is the class of stationary iterative methods for solving the system Ax^* = b. 
• Parallel implementations of the PCG algorithm

The parallel conjugate gradient algorithm involves the following  type of computations and communications

Partitioning of a matrix : The matrix A is obtained by discretization of partial differential equations by finite element, or finite difference method. In such cases, the matrix is either sparse or banded. Consequently, the partition  of the matrix onto p processes play a vital role for performance. For, simplicity , we assume that A is symmetric positive definite and is rowwise block-striped partitioned. 


Scalar Multiplication of a vector and addition of vectors :
Each of these computations can be performed sequentially regardless of the preconditioner and the type of coefficient matrix. If all vectors are distributed identically among the processes, these steps require no communication in a parallel implementation.

Vector inner products :
In some situations, partial vectors are available on each  processes.  MPI Collective library calls are necessary to perform vector inner products  If the parallel computer supports fast reduction operations, such as optimized MPI, then the communication time for the inner-product calculations can be made minimum.

Matrix-vector multiplication :
The computation and the communication cost of the matrix-vector multiplication; depends on the structure of the matrix A. The parallel implementation of the PCG algorithm for three cases one in which A is a block-tridiagonal matrix of the type, two in which it is banded unstructured sparse matrix, and three in which the matrix is sparse give different performance on parallel computers. Various parts of the algorithm in each of the three cases dominate in terms of communication overheads.

Solving the preconditioned system :
The PCG algorithm solves system of linear equations in each iteration The preconditioner C is chosen so that solving the system modified system is in expensive compared to solving the original system of equations Ax = b. Nevertheless, preconditioning increases the amount of computation in each iteration. For good preconditioners, however, the increase is compensated by a reduction in the number of iterations required to achieve acceptable convergence. The computation and the communication requirements of this step depends on the type of preconditioner used. preconditioning method such as diagonal preconditioning, in which the preconditioning matrix C has nonzero elements only along the principle diagonal does not involve any communication Also, Incomplete Cholesky (IC) preconditioning, in which C is based on incomplete Cholesky factorization of A and it may involve different computations and communications in parallel implementation.

The convergence of CG method iterations performed by checking the error criteria i.e. eulicidean norm of the residual vector should be less than prescribed tolerance. This convergence check involves gathering of real value from all processes, which may be very costly operation.

We consider parallel implementations of the PCG algorithm using diagonal preconditioner for dense coefficient matrix type. As we will see, if C is a diagonal preconditioner, then solving the modified system does not require any interprocessor communication. Hence, the communication time in a CG iteration with diagonal preconditioning is the same as that in an iteration of the unpreconditioned algorithm.

Thus the operations that involve any communication overheads are computation of inner products, matrix-vector multiplication and, in case of IC preconditioner solving the system.

• Input

  Input Matrix and Right Hand side Vector

• Output

  Solution x of linear system of matrix equations Ax = b

• Objective

  To write a CUBLAS CUDA program on sparse matrix multiplication of size n x n and vector of size n.
  

• Efficient storage format for sparse matrix

  Dense matrices are stored in the computer memory by using two-dimensional arrays. For example, a matrix with n rows and m columns, is stored using a n x m array of real numbers. However, using the same two-dimensional array to store sparse matrices has two very important drawbacks. First, since most of the entries in the sparse matrix are zero, this storage scheme wastes a lot of memory. Second, computations involving sparse matrices often need to operate only on the non-zero entries of the matrix. Use of dense storage format makes it harder to locate these non-zero entries. For these reasons sparse matrices are stored using different data structures.
  
  The Compressed Row Storage format (CRS) is a widely used scheme for storing sparse matrices. In the CRS format, a sparse matrix A with n rows having k non-zero entries is stored using three arrays: two integer arrays rowptr and colind, and one array of real entries values. The array rowptr is of size n+1, and the other two arrays are each of size k. The array colind stores the column indices of the non-zero entries in A, and the array values stores the corresponding non-zero entries. In particular, the array colind stores the column-indices of the first row followed by the column-indices of the second row followed by the column-indices of the third row, and so on. The array rowptr is used to determine where the storage of the different rows starts and ends in the array colind and values. In particular, the column-indices of row i are stored starting at colind [rowptr[i]] and ending at (but not including) colind [rowptr[i+1] ]. Similarly, the values of the non-zero entries of row i are stored at values [rowptr[i] ] and ending at (but not including) values [rowptr[i+1] ]. Also note that the number of non-zero entries of row i is simply rowptr[i+1]-rowptr[i].

• Serial sparse matrix vector multiplication

  The following function performs a sparse matrix-vector multiplication [y]={A} {b} where the sparse matrix A is of size n x m, the vector b is of size m and the vector y is of size n. Note that the number of columns of A (i.e., m ) is not explicitly specified as part of the input unless it is required.

  void SerialSparseMatVec(int n, int *rowptr, int *colind, double *values
  double *b, double  *y)   
  { 
        int i, j, count ;  
        count = 0;
        for(i=0; i<n; i++)
        {
          y[i] = 0.0;
          for (j=rowptr[i]; j<rowptr[i+1];   j++)
            y[i] += value [count] * b [colind[j]];
          count ++;
        }
  }
  
  

• Description of parallel algorithm

  In the parallel implementation, each thread picks a row from the matrix and multiplies it with the vector. Thus computation of all threads is carried out in parallel.

• Implementation

  There are two implementations, one using CUDA kernels and the other using CUDPP library.
  
  CUDA implementation
  
  Step 1: The matrix size(no. of rows) and sparsity(percentage of non-zero) are provided by the user in the cmd line.
  
  Step 2: A sparse matrix and a vector of the given size are allocated and initialized. Also the row_ptr and col_idx vectors are created and assigned their appropriate based on the sparse matrix
  
  Step 3: The above vectors are also created and initialized on the device (GPU).
  
  Step 4: The sparse_matrix and vector are multiplied in the GPU to obtain the result.
  
  CUDPP implementation
  
  Steps 1 and 2 are same as above
  
  Step 3: Only two vectors are allocated on the Device-GPU, the vector to be multiplied and a vector to store the result.
  
  Step 4: A sparse matrix object is created using CUDPPHandle (object pointer) and a CUDPPConfiguration (a structure containing the specifications of the algorithm, in this case sparse_matrix vector multiplication).
  
  Step 5: The multiplication of sparse matrix and vector are performed calling the CUDPP library procedure cudppSparseMatrixVectorMultiply() which perfroms the mulitiplication in the GPU.

• CUDA API used:

  cudaMalloc(void** array, int size)      
  // allocates memory on device
  
  cudaFree(void* array )       
  // frees memory allocated on device
  
  cudaMemcpy((void*)device_array, (void*)host_array, size , cudaMemcpyHostToDevice )    
  // copies from host to device
  
  cudaMemcpy((void*)host_array, (void*)device_array, size , cudaMemcpyDeviceToHost )
  // copies from device to host
  
  

• CUDPP API used:

  cudppSparseMatrix(&sparseMatrixHandle, config, no_of_non_zero, no_of_rows, (void *) matrix, (unsigned int *) row_ptr, (unsigned int *)col_idx);
      //this fucntion creates a sparse matrix object assigned to the sparseMatrixHandle.
  
  cudppSparseMatrixVectorMultiply(sparseMatrixHandle, result, vector);    
  // performs the multiplication

• Performance:

  The gettimeofday() function which is part of sys/time.h is used to measure the time taken for computation.
  
  

• Input

The input to the problem is given as arguments in the command line. It should be given in the following format ; Suppose that the number of rows of the sparse matrix is n (only square matrices are considered) and the sparsity i.e. the percentage of number of zero's (given in the range 0 to 1) is m, then the program must be run as,

./program_name n m

CPU generates the sparse matrix, the vector to be multiplied using random values and the row_ptr and col_idx vectors based on the sparse matrix.

• Output

The CPU prints the time taken for the computation.

• Objective

  Write a CPU-GPU CUDA Program to extract performance of matrix matrix multiplication by performing computations on host-CPU & Device-GPU
  

• Description

  Two input matrices are generated on the host-CPU In simple algorithm, the input matrix is partitoned into two different blocks to perform comptuations on host-CPU ↦ device-GPU as per Grid of thread blocks. The CUBLAS3 library call performs computation on the Device-GPU and vendor supplied DGEMM libraries such as intel MKL perform computations on host-CPU.

• Input

Size (Row size, Column size) of the Input matrices and their elements.

• Output

Performance in terms of GFlops.

• Objective

  Write a CUDA program for matrix into matrix multiplication using vendour supplied CUDA BLAS libraries (DGEMM) and extract the performance in terms of Gflops.
  

• Description

  Memory is allocated for two input matrics on host-cpu and device-gpu. Initialized input matrices on host-cpu.Inputs matrics are copied from host-cpu to device-gpu.Then CUBLAS3 library function DGEMM is called to performs matrix-matrix computation on the Device-GPU. The resultant matrix is copied back from device-gpu to host-cpu.

• Input

Size of the matrix row size, matrix column size

• Output

Time Taken for computation , Gflop/s

• Objective

  Performance of Matrix Matrix Multiplication

• Description

  Provided are 3 functions to show Matrix Matrix Multiplicaiton performance on GPU's. Each function exploits various hardware features of GPU's to gain performance. One can notice performance will double each time as one goes from executing from function 1 to 3.
  Features that are exploited:
  1)Block Size 2)Thread Mapping 3)Shared Memory 4)Global Memory Bandwidth 5)Registers 6)Scheduling 7)Tiling
  Lower <function numbers> may not exploit all these features (or to a lesser degree) but as the <function number> increases features will be exploited more agressively.
  Function Name: matMulBlockwise<function number> - function that performs matrix matrix multiplication

• Input

Set <Square Matrix Size> <Shared Memory Size> <GPGPU Device Number> <Function Number>
1) <Shared Memory Size> can only take 16, 32, 48 as values
2) <Function Number> can only take 1, 2, 3 as values

• Output

Time taken and gflops for Matrix Matrix Multiplication in individual function runs based on <Function Number>.