|
hyPACK-2013 : Programming on HPC GPU Cluster : MPI & OpenCL Prog.
|
|
High Performance computing GPU Cluster (HPC GPU Cluster) is based on integration of different
programming paradigms on host-CPU
and device-GPU is available for laboratory sessions.
A prototype HPC GPU Cluster supports various heterogeneous programming features and it can be
made "adaptive" to the application it is running, assigning
the most effective resources in real-time as per application demands, without requiring
modifications to the
application that is written using different progrmaming is used.
The goal of this heterogeneous CPU-GPU mixed programming environment is to provide total
workflow optimization, which takes
cares-off applications
that do not parallelize well on scalar processors, can be optimized with the appropriate
computation model.
|
Example 1.1
|
Write MPI - OpenCL program to perform prefix sum of multiple arrays
on multiple GPUs of HPC Cluster.
|
Example 1.2
|
Write MPI - OpenCL program to compute dot product of two vectors using
block-striped partitioning with uniform data distribution.
( Assignment)
|
Example 1.3
|
Write MPI - OpenCL program to compute the Matrix and Vector Multiplication
using block-striped row-wise partitioning with uniform data distribution.
( Assignment)
|
|
Example 1.4
|
Demonstrate performance of SHOC (MPI+OpenCL)open source Software on hetrogenous computing system.(Assignment)
|
|
The HPC GPU Cluster aim is
to develop system software and integrate components OpenCL GPU
and demonstrare some of the programs in Mode-2.
Different programming paradigms on host CPU i.e. MPI, OpenMP, Pthreads and OpenCL
on GPUs are integrated and several
example programs for Dense Matrix Computations, Solution of Partial Differential
equations are considered.
|
|
Example 1.1: |
Write a MPI - OpenCL program in which each MPI process compute the pefix sum of
each array on each GPU for given number of arrays asscociate with number of processes.
(Download source code :
WinRAR ZIP archive (.zip)
)
|
- Objective
Write a MPI - OpenCL program, to compute the pefix sum of each array for given
number of arrays in which each MPI process is binding to each GPU.
- Description
Given total number of arrays binding to the number of proceses spawned in the MPI
program, each MPI process rank reads the input array and
OpenC kernel performs prefix sum of an array on each GPU asociated with MPI process rank.
-
Input
The input to the problem is given as arguments in the command line.
-
Output
Each Process 0 prints the final prefix sum of an array.
|
|
Example 1.2: |
Write MPI - OpenCL program to compute dot product of two vectors using
block-striped partitioning with uniform data distribution.
|
- Objective
Write a MPI - OpenCL program, to compute the vector-vector multiplication
on p processes of a message passing cluster using block-striped partitioning
with uniform data distribution where each processes invokes Vector Vector Multiplication
OpenCL kernel to compute the product. Assume that the vectors are of size n and p is
number of processes used and n is divisible p.
- Description
The partitioning is called block-striped if each process is assigned
contiguous elements. The process P0 gets the first n/p elements,
P1 gets the next n/p elements and so on. The distribution of 16
elements of vector A on 4 processes is shown in the following figure 1.
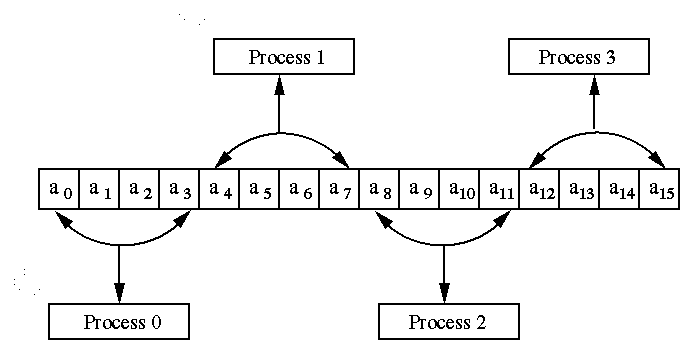Figure 1 A Typical block-striped partitioning of a vector of size 16 on 4 processes
Initially process with rank 0 distributes the input vectors
using MPI_Scatter on p processes. Each process will call a
OpenCL kernel which performs local dot product of the vectors and
stores the partial dot product. Now the process with rank 0
performs global reduction using MPI_Reduce
to get the final dot product of two vectors
-
Implementation of Vector Vector Multiplication :
Step 1 : Four vectors are required for computation. Two vectors for vector A and
Vector B and the other two for storing part of these two vectors at the each node.
Step2 : Root Processor Initializes the two vectors i.e Vector A and Vector B. The two vectors
are constructed by assigning to each element one more than its index value .
Step 3 : Vector Size is broadcasted to all nodes from the root processor.
Step 4 : Memory is assigned for MyVectorA and MyVectorB on all nodes.
Step 5 : Process with rank 0 distributes the input vectors using MPI_Scatter on to p
processes
Step 6 : Similar arrays are allocated on the device. The values of the arrays in the host machine are
copied on to the arrays allocated on the device.
Step 7 : Each node computes the partial product value by calling VectorVectorDotProduct OpenCL kernel.
Step 8 : Process with rank 0 performs global reduction using MPI_Reduce to get the final dot product of two vectors.
Step 9 : Process with rank 0 prints the product value.
-
Input
The input to the problem is given as arguments in the command line.
It should be given in the following format ;
Suppose that the size of the vector is n and the number of
nodes is m, then the program must be run as,
mpirun -n m ./program_name n
Processor 0 generates the two vectors i.e Vector A and Vector B.
-
Output
Process 0 prints the final product value of two vectors.
The product of the given two vectors is 204.0.
The correctness of the output can be verified using the below formula
The sum of the squares of the first n numbers is (n(n+1)(2n+1))/6.
|
|
Example 1.3: |
Write MPI - OpenCL program to compute the Matrix and Vector Multiplication
using block-striped row-wise partitioning with uniform data distribution
|
- Objective
Write a MPI - OpenCL program, for computing the matrix -vector
multiplication on p processors of a message passing cluster
using block striped partitioning of a matrix.
- Description
In the striped partitioning of a matrix, the matrix is
divided into groups of contiguous complete rows or columns,
and each processor is assigned one such group. The partitioning is
called block-striped if each processor is assigned contiguous rows or
columns. Striped partitioning can be block or cyclic.
In a row-wise block striping of an nxn matrix on p processors
(labeled P0 , P1, P2,..., P p-1 ) , processor Pi contains rows with indices (n/p)i,
(n/p)i+1, (n/p)i+2, (n/p)i+3,........, (n/p)(i+1)-1. A typical column-wise or
row-wise partitioning of 16 x 16 matrix on
4 processors is shown in the following Figure 2.
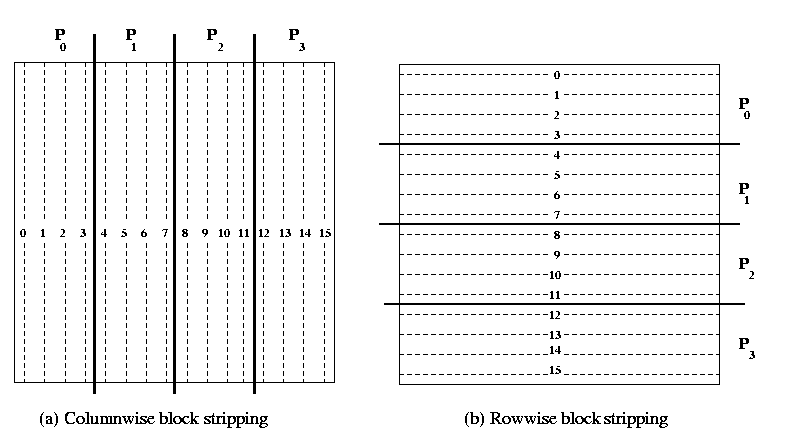Figure 2 Uniform block-striped partitioning of 16 x 16 matrix on 4 processors.
The matrix A of size n x n is striped row-wise among p processes so
that each process stores n/p rows of the matrix. We assume that the vector
x of size n x 1 is available on each process . Now, process Pi computes
the dot product of the corresponding rows of the matrix A[*] with the vector B[ * ]
by calling the OpenCL kernel Matrix Vector Multiplication and accumulate the partial
result in the vector My Result vector[ * ]. Finally, process P0 collects the dot
product of different rows of the matrix with the vector from all the processes.
-
Implementation of Matrix Vector Multiplication :
Step 1 : Five arrays are required for computation. One each, for
storing Matrix, vector, result vector, some part of the Matrix and the some part of the result vector.
Step 2 : Root processor initializes the Matrix, vector and the resultant vector.
The matrix and the vector are constructed by assigning one to each element and the result vector is initialized to zero.
Step 3: Vector B is broadcasted to all the processors from the root node.
Step 4 : Scatter size is computed.
Step 5 : Memory is allocated for MyMatrixA and the MyResultVector by all the nodes.
Step 6 : Process with rank 0 distributes the Matrix using MPI_Scatter on to p processes.
Step 7 : Similar vectors are allocated on the device. The values of the vectors in the host machine are copied to the vectors on
the device machine.
Step 8 : Each node computes the Matrix vector multiplication by calling the OpenCL kernel MatrixVectorMultiplication and copies back the result to
MyResultVector on the host.
Step 9 : Processor 0 gathers from all the nodes and form the final result vector.
Step10 : Process with rank 0 prints the resultant vector.
-
Input
The input to the problem is given as arguments in the command line.
It should be given in the following format .
Suppose the dimension of the matrix is mxn, size of the vector is n
and the number of processors is p.
mpirun -n p ./Matrix_Vector_Multiply m n n
Process with rank 0 generates the Matrix and the vector.
-
Output
Process 0 prints the final vector.
|
|
Example 1.4: |
Demonstrate performance of SHOC(MPI+OpenCL) open source Software on hetrogenous computing system.
|
|
|
|
|
