|
hyPACK-2013 : Prog. on HPC GPU Cluster : MPI & CUDA Prog.
|
|
High Performance computing GPU Cluster (HPC GPU Cluster) is based on integration of different
programming paradigms on host-CPU
and device-GPU is available for laboratory sessions.
A prototype HPC GPU Cluster supports various heterogeneous programming features and it can be
made \93adaptive\94 to the application it is running, assigning
the most effective resources in real-time as per application demands, without requiring
modifications to the
application that is written using different progrmaming is used.
The goal of this heterogeneous CPU-GPU mixed programming environment is to provide total
workflow optimization, which takes
cares-off applications
that do not parallelize well on scalar processors, can be optimized with the appropriate
computation model.
|
|
Example 1.1
|
Write MPI \96 CUDA program to compute dot product of two vectors using
block-striped partitioning with uniform data distribution.
|
|
Example 1.2
|
Write MPI \96 CUDA program to compute dot product of two vectors on Multi-GPUs
|
|
Example 1.3
|
Write MPI \96 CUDA program to compute the Matrix and Vector Multiplication
using block-striped row-wise partitioning with uniform data distribution.
|
|
Example 1.4
|
Demonstrate performance of LINPACK CUDA Software on NVIDIA GPU.(Assignment)
|
|
Example 1.5
|
Demonstrate performance of SHOC (MPI+cuda) open source Software on hetrogenous computing system.(Assignment)
|
|
The HPC GPU Cluster is used in Hand-on to support various programming paradigms such as
MPI, OpenMP, MPI on Host CPU
and integrate with CUDA 5.0 enabled NVIDIA GPU and OpenACC. Several
example programs for Dense/Sparse Matrix Computations involving Iterative methods, and Solution of
Partial Differential equations are included.
|
- Objective
Write a MPI \96 CUDA program, to compute the vector-vector multiplication
on p processors of a message passing cluster using block-striped partitioning
with uniform data distribution where each processor invokes Vector Vector Multiplication
CUDA kernel to compute the product. Assume that the vectors are of size n and p is
number of processes used and n is divisible p.
- Description
The partitioning is called block-striped if each process is assigned
contiguous elements. The process P0 gets the first n/p elements,
P1 gets the next n/p elements and so on. The distribution of 16
elements of vector A on 4 processes is shown in the following figure 1.
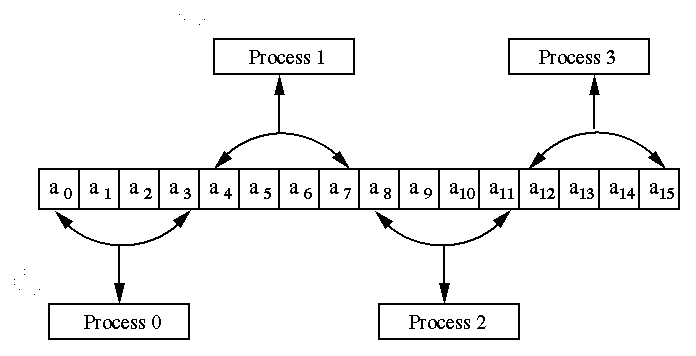Figure 1 A Typical block-striped partitioning of a vector of size 16 on 4 processes
Initially process with rank 0 distributes the input vectors
using MPI_Scatter on p processes. Each process will call a
CUDA kernel which performs local dot product of the vectors and
stores the partial dot product. Now the process with rank 0
performs global reduction using MPI_Reduce
to get the final dot product of two vectors
-
Implementation of Matrix Vector Multiplication :
Step 1 : Four vectors are required for computation. Two vectors for vector A and
Vector B and the other two for storing part of these two vectors at the each node.
Step2 : Root Processor Initializes the two vectors i.e Vector A and Vector B. The two vectors
are constructed by assigning to each element one more than its index value .
Step 3 : Vector Size is broadcasted to all nodes from the root processor.
Step 4 : Memory is assigned for MyVectorA and MyVectorB on all nodes.
Step 5 : Process with rank 0 distributes the input vectors using MPI_Scatter on to p processes
Step 6 : Similar arrays are allocated on the device. The values of the arrays in the host machine are c
opied on to the arrays allocated on the device.
Step 7 : Each node computes the partial product value by calling VectorVectorDotProduct CUDA kernel.
Step 8 : Process with rank 0 performs global reduction using MPI_Reduce to get the final dot product of two vectors.
Step 9 : Process with rank 0 prints the product value.
-
CUDA API used :
To Allocate memory on device-GPU :
cudaMalloc(void** array, int size)
To Free memory allocated on device-GPU:
cudaFree(void* array)
To transfer from host-CPU to device-GPU:
cudaMemcpy((void*)device_array, (void*)host_array, size, cudaMemcpyHostToDevice)
To transfer from device-GPU to host-GPU:
cudaMemcpy((void*)host_array, (void*)device_array, size, cudaMemcpyDeviceToHost)
-
Input
The input to the problem is given as arguments in the command line.
It should be given in the following format ;
Suppose that the size of the vector is n and the number of
nodes is m, then the program must be run as,
mpirun -n m ./program_name n
Processor 0 generates the two vectors i.e Vector A and Vector B.
A sample Vectors for the size 8 is given below:
-
Output
Process 0 prints the final product value of two vectors.
The product of the given two vectors is 204.0.
The correctness of the output can be verified using the below formula
The sum of the squares of the first n numbers is (n(n+1)(2n+1))/6.
|
- Objective
Write a MPI \96 CUDA program, to compute the vector-vector multiplication
on Multi-Core processor system with multi-GPU.
Assume that each process computes the partial Vector Vector Multiplication
using CUDA kernel.
- Description
The partitioning is called block-striped if each process is assigned
contiguous elements. The process P0 gets the first n/p elements,
P1 gets the next n/p elements and so on. The distribution of 16
elements of vector A on 4 processes is shown in the following figure 1.
Figure 1 A Typical block-striped partitioning of a vector of size 16 on 4 processes
Initially process with rank 0 distributes the input vectors
using MPI_Scatter on p processes. Each process will call a
CUDA kernel which performs local dot product of the vectors and
stores the partial dot product. Now the process with rank 0
performs global reduction using MPI_Reduce
to get the final dot product of two vectors
-
Implementation of Vector Vector Multiplication :
Step 1 : Four vectors are required for computation. Two arrays for vector A and
Vector B and the other two arrays for temporary storage data fortwo vectors at
the each node.
Step2 : Root process initializes the two vectors i.e Vector A and Vector B. The
two vectors
are constructed by assigning to each element one more than its index value .
Step 3 : Vector Size is broadcasted to all processes from the root process.
Step 4 : Memory is assigned for MyVectorA and MyVectorB on all nodes.
Step 5 : Process with rank 0 distributes the input vectors using MPI_Scatter on to p processes
Step 6 : Similar arrays are allocated on the device. The values of the arrays in the host machine are c
opied on to the arrays allocated on the device.
Step 7 : Each node computes the partial product value by calling VectorVectorDotProduct CUDA kernel.
Step 8 : Process with rank 0 performs global reduction using MPI_Reduce to get the final dot product of
two vectors.
Step 9 : Process with rank 0 prints the product value.
-
CUDA API used :
To Allocate memory on device-GPU :
cudaMalloc(void** array, int size)
To Free memory allocated on device-GPU:
cudaFree(void* array)
To transfer from host-CPU to device-GPU:
cudaMemcpy((void*)device_array, (void*)host_array, size, cudaMemcpyHostToDevice)
To transfer from device-GPU to host-GPU:
cudaMemcpy((void*)host_array, (void*)device_array, size, cudaMemcpyDeviceToHost)
-
Input
The input to the problem is given as arguments in the command line.
It should be given in the following format ;
Suppose that the size of the vector is n and the number of
nodes is m, then the program must be run as,
mpirun -n m ./program_name n
Process 0 generates the two vectors i.e Vector A and Vector B.
-
Output
Process 0 prints the final product value of two vectors.
The product of the given two vectors is 204.0.
The correctness of the output can be verified using the below formula
The sum of the squares of the first n numbers is (n(n+1)(2n+1))/6.
|
- Objective
Write a MPI - CUDA program, for computing the matrix -vector
multiplication on p processors of a message passing cluster
using block striped partitioning of a matrix.
- Description
In the striped partitioning of a matrix, the matrix is
divided into groups of contiguous complete rows or columns,
and each processor is assigned one such group. The partitioning is
called block-striped if each processor is assigned contiguous rows or
columns. Striped partitioning can be block or cyclic.
In a row-wise block striping of an nxn matrix on p processors
(labeled P0 , P1, P2,..., P p-1 ) , processor Pi contains rows with indices (n/p)i,
(n/p)i+1, (n/p)i+2, (n/p)i+3,........, (n/p)(i+1)-1. A typical column-wise or
row-wise partitioning of 16 x 16 matrix on
4 processors is shown in the following Figure 2.
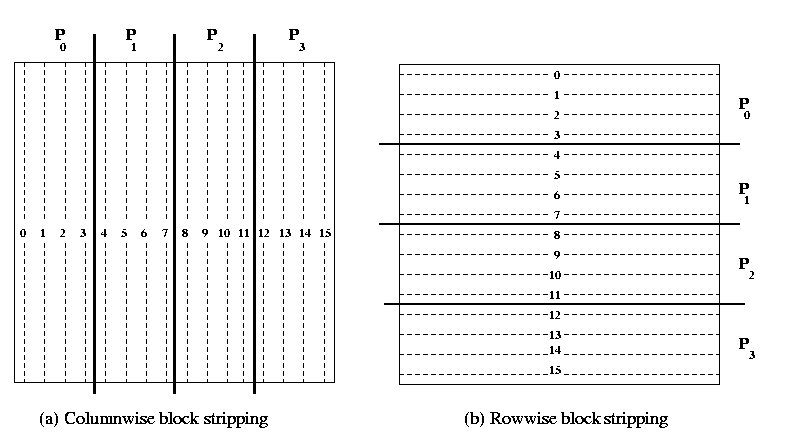Figure 2 Uniform block-striped partitioning of 16 x 16 matrix on 4 processors.
The matrix A of size n x n is striped row-wise among p processes so
that each process stores n/p rows of the matrix. We assume that the vector
x of size n x 1 is available on each process . Now, process Pi computes
the dot product of the corresponding rows of the matrix A[*] with the vector B[ * ]
by calling the CUDA kernel Matrix Vector Multiplication and accumulate the partial
result in the vector My Result vector[ * ]. Finally, process P0 collects the dot
product of different rows of the matrix with the vector from all the processes.
-
Implementation of Matrix Vector Multiplication :
Step 1 : Five arrays are required for computation. One each, for
storing Matrix, vector, result vector, some part of the Matrix and the some part of the result vector.
Step 2 : Root processor initializes the Matrix, vector and the resultant vector.
The matrix and the vector are constructed by assigning one to each element and the result vector is initialized to zero.
Step 3: Vector B is broadcasted to all the processors from the root node.
Step 4 : Scatter size is computed.
Step 5 : Memory is allocated for MyMatrixA and the MyResultVector by all the nodes.
Step 6 : Process with rank 0 distributes the Matrix using MPI_Scatter on to p processes.
Step 7 : Similar vectors are allocated on the device. The values of the vectors in the host machine are copied to the vectors on
the device machine.
Step 8 : Each node computes the Matrix vector multiplication by calling the CUDA kernel MatrixVectorMultiplication and copies back the result to
MyResultVector on the host.
Step 9 : Processor 0 gathers from all the nodes and form the final result vector.
Step10 : Process with rank 0 prints the resultant vector.
-
CUDA API used :
To Allocate memory on device-GPU :
cudaMalloc(void** array, int size)
To Free memory allocated on device-GPU:
cudaFree(void* array)
To transfer from host-CPU to device-GPU:
cudaMemcpy((void*)device_array, (void*)host_array, size, cudaMemcpyHostToDevice)
To transfer from device-GPU to host-GPU:
cudaMemcpy((void*)host_array, (void*)device_array, size, cudaMemcpyDeviceToHost)
-
Input
The input to the problem is given as arguments in the command line.
It should be given in the following format .
Suppose the dimension of the matrix is mxn, size of the vector is n
and the number of processors is p.
mpirun -n p ./Matrix_Vector_Multiply m n n
Process 0 generates the Matrix and the vector.
-
Output
Process 0 prints the final vector.
|
|
Example 1.5: |
Demonstrate performance of SHOC open source Software on hetrogenous computing system.
|
|
|
|
|
